Five-Step Strategy for Problem Solving in Physics

The Five-Step Strategy is a forward problem-solving method grounded in physics principles.
It’s based on research in physics education and cognitive science, and captures what the most effective strategies have in common—without unnecessary complexity.

Many students intuitively use parts of this process, but often skip key steps that make problem solving both faster and more reliable. One of the most important—and most overlooked—is Step 3: Physics Modeling.

The core problem-solving framework from Masterful Learning. The book includes worked examples, common pitfalls, and exam-specific applications.

---

Example: Five-Step Strategy in Action

Problem. A 65-kg ninja in an obstacle course competition runs at a speed of 4.0 m/s and then slides down a 2.0-meter-high frictionless ramp. At the bottom of the ramp, the ninja collides with a 35-kg sack hanging straight down from a 5.0-meter-long rope (assume the rope is massless). By holding on to the sack, the ninja swings upward toward a platform. What is the tension in the rope immediately after the collision?

Step 1: Verbal Decoding

Target: $T$
Given: $m_n, m_s, v_0, h, r$.

Step 2: Visual Decoding

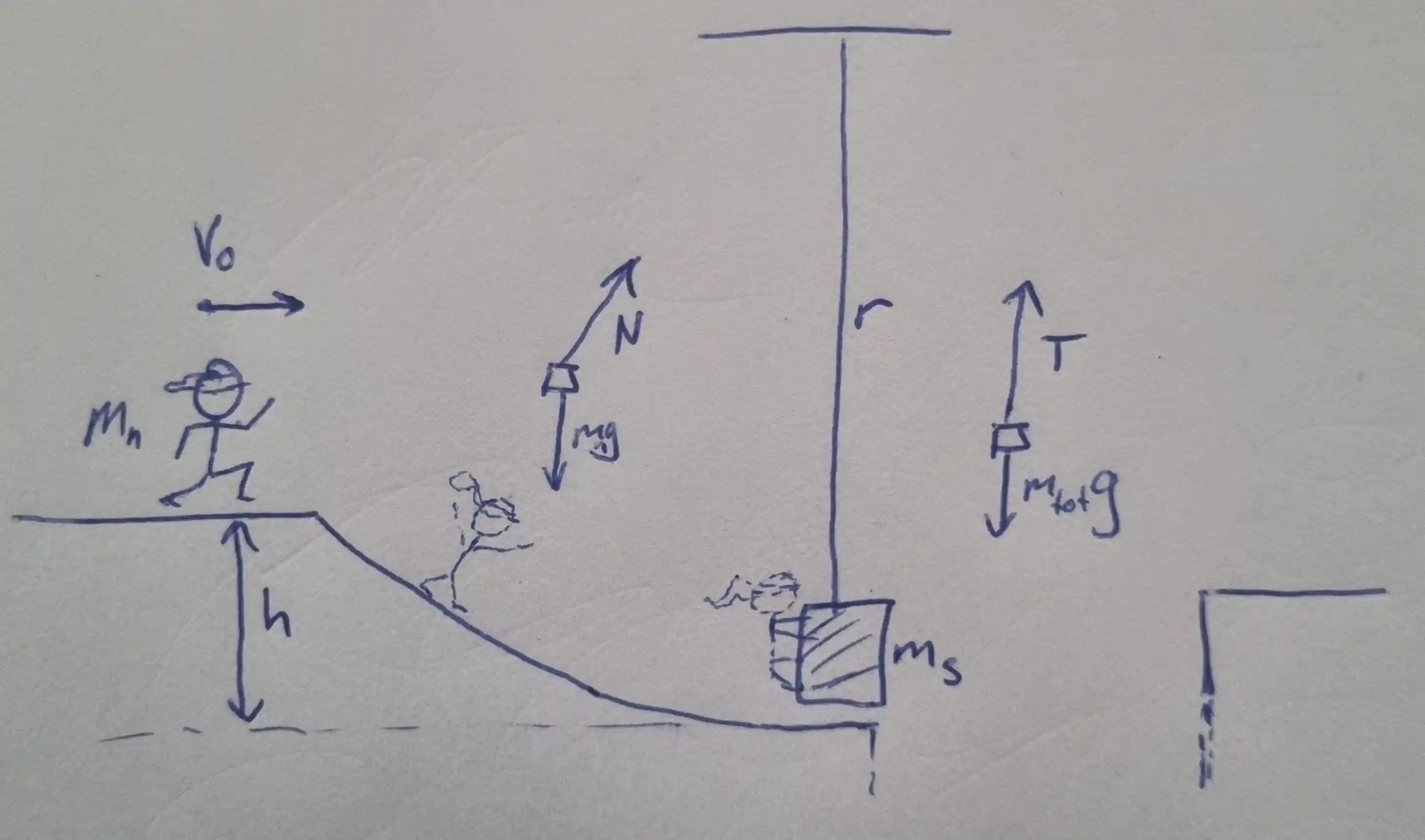
Step 3: Physics Modeling

$$\tfrac12 m_n v_0^2 + m_n g h = \tfrac12 m_n v_1^2$$ $$m_n v_1 = m_{\text{tot}} v_2$$ $$\sum F_y = T - m_{\text{tot}} g = m_{\text{tot}} \frac{v_2^2}{r}$$

Step 4: Mathematical Procedures

$$v_0^2 + 2gh = v_1^2$$ $$v_1 = \sqrt{v_0^2 + 2gh}$$ $$v_1 = \sqrt{(4.0)^2 + 2(9.8)(2.0)} = 7.4\ \mathrm{m/s}$$ $$v_2 = \frac{m_n}{m_{\text{tot}}} v_1$$ $$v_2 = \frac{65}{100} \times 7.4 = 4.8\ \mathrm{m/s}$$ $$T = m_{\text{tot}}\left(g + \frac{v_2^2}{r}\right)$$ $$T = 100\left(9.8 + \frac{(4.8)^2}{5.0}\right) = 1.44 \times 10^3\ \mathrm{N}$$

Step 5: Reflection

Dimensional analysis: $[N]=\mathrm{kg\,m\,s^{-2}}$ ✓

Size assessment: $T\approx 1.4\,\mathrm{kN}$ (about $1.5\times$ weight, $980\,\mathrm{N}$) — realistic right after impact.

Interpretation: $T$ increases with $v_2$ (quadratic), decreases with larger $r$; heavier sack raises $m_{\text{tot}}$ but lowers $v_2$, pushing $T$ toward $m_{\text{tot}}g$ in the heavy-sack limit.

---

Continue Learning

Master the technique: For a deeper understanding of how to explain each step in your reasoning process, see our guide on self-explanation — the most effective learning strategy for solving new types of problems.

Go deeper: For comprehensive coverage of problem-solving strategies in physics, math, and programming, check out Masterful Learning — a research-backed approach to developing expertise in any domain.

---

Step 1: Verbal Decoding

Identify the target and given variables.
Some are explicit (“a block with mass 0.100 kg”), others require inference (e.g., “moves at constant speed” → acceleration = 0).

Write them down as:

Target: $\langle$target variables$\rangle$
Given: $\langle$given variables$\rangle$

Skip numerical values at this stage—stay focused on structure, not computation.
This primes your brain to recognize relevant concepts before moving to modeling.

---

Step 2: Visual Decoding

Transform the situation into visual form to reduce working memory load.
This can include:

• Situation sketches – show objects and variables, compacting complexity.
• Diagrams – especially free-body diagrams, which clarify forces and directions.
• Graphs – such as velocity–time or force–displacement, for identifying trends.

Why it matters: Visual tools aren’t just decoration—they’re core thinking aids for physicists. They make modeling easier, help you spot patterns, and reduce mistakes.

---

Step 3: Physics Modeling

With verbal and visual decoding done, apply physics principles to describe the situation in solvable mathematical terms.
On most exams, a correct model is worth 80–90% of the points—even before calculating.

3.1 Check the conditions

Ask:

• Is acceleration constant?
• Are only conservative forces doing work?
• Is net force or torque zero?

3.2 Select principles

Match the conditions to principles:

• Newton’s Second Law if acceleration is non-zero and force/mass are relevant.
• Energy conservation if only conservative forces act.
• Momentum conservation if the system is isolated.

3.3 Build the mathematical model

Translate principles into equations:

• Use your free-body diagram to project forces along axes.
• For energy, write expressions for kinetic and potential energy at key points.
• Keep equations symbolic; avoid plugging numbers too soon.

Tip: When learning, include all applicable principles, then simplify. This builds the mental library of “solution rules” you’ll later retrieve automatically.

---

Step 4: Mathematical Procedures

Now solve the model for the target variables.
Often this means n equations for n unknowns, solved via algebra.

Best practices:

• Work symbolically as long as possible.
• Rearrange and substitute step-by-step.
• Compute intermediate values to check plausibility.

Symbolic manipulation is essential for recognizing mistakes and enabling interpretation of the physics in the reflection stage.

---

Step 5: Reflection

Before finalizing your answer:

1. Dimensional analysis – check that units match on both sides of the equation.
2. Size evaluation – ask if the magnitude is realistic.
3. Interpretation – look for insights (mass cancels, dependence on height only, etc.).

Why it matters: Reflection catches avoidable errors and deepens your conceptual grasp.

---

Key Takeaways

• Don’t skip steps. Each stage builds on the previous.
• Model first, calculate second. Equations without a correct model are wasted effort.
• Reflect to learn. Understanding why your solution works is as important as getting the right number.
• Explain your reasoning. Use self-explanation techniques throughout each step to deepen your understanding and catch errors.

---

Next step:
Choose a physics problem from your current topic, and run through all five steps—without skipping. Over time, the process will become automatic, and your speed and accuracy will both improve.